DERIVADAS PARCIALES

Las derivadas parciales de una función con varias variables f(x , y, z) (tres en este caso) nos informa de cómo cambia la función (df) cuando se produce un pequeño cambio en una única variable independiente (por ejemplo dx en la variable x).

Como ahora no estamos ante una función y = f(x) que varía, cuando cambia la única variable independiente x de esa función, sino que hay varias variables, para subrayar que se trata de cambios en la función multivariable utilizaremos el símbolo  ∂   para distinguirlo del símbolo d, que es el que indica un pequeño cambio en el caso de las funciones ordinarias.  

Las derivadas parciales de una función multivariable las definiremos también mediante un límite, si   límite existiera, haciendo extensiva la definición de una derivada ordinaria.

  Las derivadas parciales de una función u = f(x , y, z) serían:

• En el primer caso, la derivada parcial de la función respecto a x, se consideran las variables independientes y y z como unas constantes.                                                

• En el segundo caso, respecto a y, se consideran las variables independientes x y z como unas constantes.                                                                        

• En el tercer caso, la derivada parcial de la función respecto a z, se consideran las variables independientes x e y como unas constantes.

• En la imagen de arriba se ha puesto en azul la variable sobre la que se obtiene la derivada parcial.

Se procederá a derivar empleando las reglas de derivación conocidas en las derivadas ordinarias.

 

Derivación implícita con derivadas parciales.

 

Derivadas parciales permiten obtener en muchas ocasiones con más sencillez derivación implícita.
La derivación implícita, se obtiene el mismo resultado en derivación implícita mediante derivadas parciales, con la siguiente fórmula que facilita y simplifica el cálculo:

ejercicio 1

                      

Ejemplo 1

Sea  una función definida en varias variables, calcule .

Para calcular esta derivada, debemos calcular primero la derivada de  respecto a la variable :

Calculamos entonces la derivada de la función  respecto a la variable .

Supongamos que queremos calcular , entonces debemos calcular la derivada de la función  respecto a la variable :

Cuando estamos aprendiendo a calcular derivadas parciales y más aún, de orden superior; es normal que uno se enrede con tantas variables. Con el diagrama que veremos a continuación se puede entender con un poco más de claridad que variables debemos considerar al derivar:

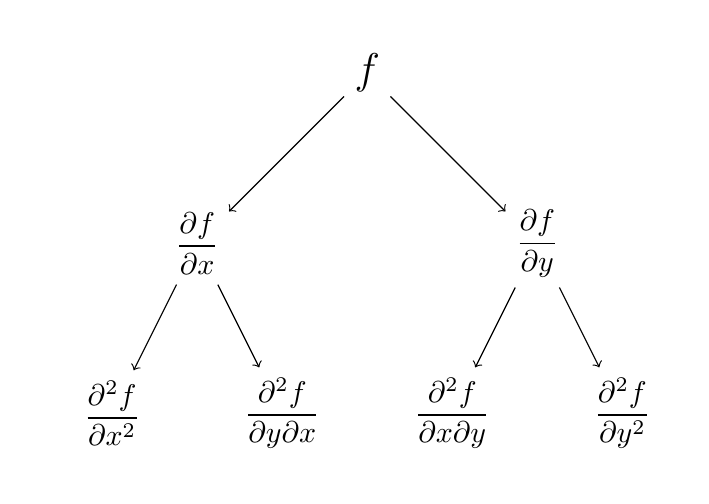
Otra notación que puede ser útil para aligerar la escritura de las derivadas parciales consiste en escribir la función y usar un subíndice sobre esta para indicar cual es la variable respecto a la cual estamos derivando de la siguiente forma:

videos

Referencias
 Formulashttps://www.universoformulas.com/matematicas/analisis/derivadas-parciales/
https://totumat.com/tag/derivadas-de-ord